A question you rightfully may be pondering is: Why translate object oriented classes into OWL? The answer is that it can help you to find logical inconsistencies in your class designs. In this post I will introduce the tools that will eventually enable you to find logical inconsistencies in your class designs.

The tool we will use is called Protégé. Download and installations instructions for Protégé can be found at https://protegewiki.stanford.edu/wiki/Install_Protege5.

In this post I will provide two screencasts:

1. In the first screencast I will show you how to enter the OWL representation of the Person class introduced in the previous post.
2. In the second screencast I will show you how to run a reasoner and how an inconsistency can arise.

On to the first screencast:

1. Create a Person class.
2. Create the data properties.
   1. name
   2. surname
   3. age
3. Through sub-classing state that the Person class necessarily have a
   1. name,
   2. surname and
   3. age.
4. If we run the reasoner on this ontology, no inconsistencies will be found.

In the second screencast I show how an inconsistency can arise. The steps are as follows:

1. Create an individual called sarah of type Person.
2. Run the reasoner. You will see the reasoner give no errors (nothing happened). This may come as a surprise to you since we have not set the name, surname or age data properties for the individual called sarah. In OWL this behaviour is expected due to what is called the open world assumption. OWL makes no assumption with regards to knowledge that is not stated explicitly. Since we did not state that the sarah individual does not have, for example, a name, the reasoner found no error in our ontology. This is different from typical database behaviour where absence of information is often assumed to indicate that the information does not exist, which is referred to as the closed world assumption.
3. Now let us change our sarah individual to state that it does not have a name. This is achieved by stating that the sarah individual is of type name max 0 xsd:string. This states that the sarah individual can have a maximum of 0 name data properties of type xsd:string.
   
4. If we run the reasoner now it shows that we have an inconsistency. We can ask Protégé to explain the inconsistency.
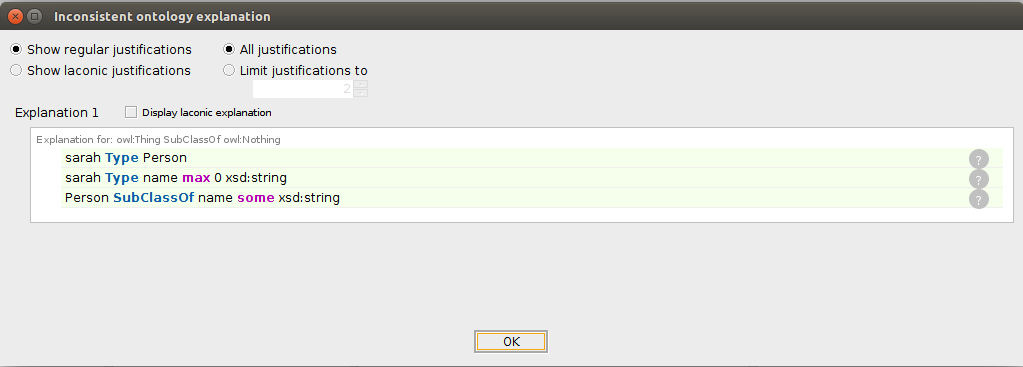
5. The explanation states that sarah is of type Person and of type name max 0 xsd:string. But Person is a subclass of name some xsd:string. This states that individuals of type Person must have at least 1 name property of type xsd:string. Hence, the reason for the inconsistency.

Admittedly this example is contrived: there is not much sense in creating a Person class which we state must have a name and then create an individual of type Person which we then state does not have a name. But this was done here to show you how to use a reasoner to find inconsistencies in your ontology and to show you what information you can expect when your ontology is inconsistent.

In this post what I want to do is add some attributes to the Person class of the previous post. The important thing to understand is that as you add attributes to a class, what you are doing in effect is adding additional constraints that will cause the number of objects that can be of that type to shrink. This is illustrated in the Venn diagram below. Note that our Person class is now a subset of the intersection of the sets of objects with name as attribute, surname as attribute and age as attribute.

If we now consider the OWL 2 representation of this class in Manchester syntax, it matches our Venn diagram exactly. It further states that name, surname and age are properties. It states that individuals of the Person class have a name property of type xsd:string, a surname property of type xsd:string and a age property of type xsd:integer.

Let us start with a simple example. Assume we have a Person class, which models a person that has a name. Let us just think about what this means. If we think of our domain of interest and we list all the objects of the domain, some objects will belong to a set that is a subset of the domain of interest, which is called the Person set, which is represented by our Person class. Our Person class also has a name attribute of type String, but it is likely that we will have other classes in our domain that may have a name attribute of type String. Thus, the Person class represents objects that are a subset of all the objects in the domain that have a name attribute of type String. This is shown in the Venn diagram below.

Note that the Person class is not necessarily a strict subset of the objects that have a name attribute of type String. It is possible that the Person class is the only class in our domain that has a name attribute of type String, in which case these two sets are in fact equal.

The OWL 2 equivalent representation in Manchester syntax is given in the image below. Note that for the name attribute in the UML class we have defined a related DataProperty. Furthermore, a Person class is also defined, which is defined as SubClassOf: name some xsd:string. What this means is that individuals that belongs to the Person class also belongs to the class of individuals that have a name property of type xsd:string. Thus, the Person class is a subclass of the class representing individuals that have a name property of type xsd:string.